Pythagoras' Theorem

Pythagoras' Theorem

Pythagoras' Theorem

Pythagoras

Over 2000 years ago there was an amazing discovery about triangles:

When a triangle has a right angle (90°) ...

... and squares are made on each of the three sides, ...

... then the biggest square has the exact same area as the other two squares put together!

It is called "Pythagoras' Theorem" and can be written in one short equation:

a2 + b2 = c2

Note:

c is the longest side of the triangle

a and b are the other two sides

Definition

The longest side of the triangle is called the "hypotenuse", so the formal definition is:

In a right angled triangle:

the square of the hypotenuse is equal to

the sum of the squares of the other two sides.

Sure ... ?

Let's see if it really works using an example.

Example: A "3,4,5" triangle has a right angle in it.

Let's check if the areas are the same:

32 + 42 = 52

Calculating this becomes:

9 + 16 = 25

It works ... like Magic!

Why Is This Useful?

If we know the lengths of two sides of a right angled triangle, we can find the length of the third side. (But remember it only works on right angled triangles!)

How Do I Use it?

Write it down as an equation:

a2 + b2 = c2

Then we use algebra to find any missing value, as in these examples:

Example: Solve this triangle

Start with:a2 + b2 = c2

Put in what we know:52 + 122 = c2

Calculate squares:25 + 144 = c2

25+144=169:169 = c2

Swap sides:c2 = 169

Square root of both sides:c = √169

Calculate:c = 13

You can also read about Squares and Square Rootsto find out why √169 = 13

Example: Solve this triangle.

Start with:a2 + b2 = c2

Put in what we know:92 + b2 = 152

Calculate squares:81 + b2 = 225

Take 81 from both sides:81 − 81 + b2 = 225 − 81

Calculate:b2 = 144

Square root of both sides:b = √144

Calculate:b = 12

Example: What is the diagonal distance across a square of size 1?

Start with:a2 + b2 = c2

Put in what we know:12 + 12 = c2

Calculate squares:1 + 1 = c2

1+1=2:2 = c2

Swap sides:c2 = 2

Square root of both sides:c = √2

Which is about:c = 1,4142...

It works the other way around, too: when the three sides of a triangle make a2 + b2 = c2, then the triangle is right angled.

Example: Does this triangle have a Right Angle?

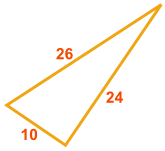
Does a2 + b2 = c2 ?

a2 + b2 = 102 + 242 = 100 + 576 = 676

c2 = 262 = 676

They are equal, so ...

Yes, it does have a Right Angle!

Example: Does an 8, 15, 16 triangle have a Right Angle?

Does 82 + 152 = 162 ?

82 + 152 = 64 + 225 = 289,

but 162 = 256

So, NO, it does not have a Right Angle

Example: Does this triangle have a Right Angle?

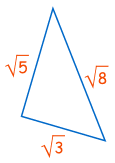
Does a2 + b2 = c2 ?

Does (√3)2 + (√5)2 = (√8)2 ?

Does 3 + 5 = 8 ?

Yes, it does!

So this is a right-angled triangle.